Se considera que dos numeros se encuentran en Proporción Aurea cuando al dividirlos obtenemos Phi, el numero de Or
Phi es un numero irracional, con muchas propiedades interesantes y no es una unidad, sino una relación o proporción ,entre segmentos y rectas.
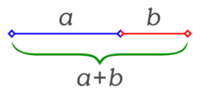
Una sección áurea es una división en dos de un segmento según proporciones dadas por el número áureo. La longitud total a+b es al segmento más largoa como a es al segmento más corto b.
"La geometría tiene dos grandes tesoros: uno es el teorema de Pitágoras; el otro, la división de una línea entre el extremo y su proporcional. El primero lo podemos comparar a una medida de oro; el segundo lo debemos denominar una joya preciosa”
Johannes Kepler en Mysterium Cosmographicum (El Misterio Cósmico)
Podemos encontrar la proporción áurea en...

-Arquitectura: en las dimensiones de la Cámara Real de la Gran Pirámide de Keops, en los planos y fachada del Partenón, en las obras de Le Corbusier, en la torre Eiffel y Notre Dame de Paris ,en la Alambra, en El Escorial, en algunas de las catedrales europeas ,en la sede de la ONU en NY, etc
-Música: en la estructura formal de algunas obras musicales de Shubert y Debussy, en las sonatas de Mozart y en la quinta sinfonía de Beethoven.
-Arte:En las obras de Durero, da Vinci, Mondrián, Dalí, en la Venus de Boticceli, en la escultura "David", de Miguel Angel, entre otros...
-En la vida moderna: la pantalla ancha de los televisores, en las tarjetas postales, en lastarjetas de crédito y del DNI,en las cajas de cigarrillos,en el frasco de Chanel nª5, en las cadenas del ADN , etc.

-En la naturaleza: en las caracolas, en las hojas de algunas plantas, en las piñas, en nuestras manos!
"Secuencia de Fibonacci" (Leonardo de Pisa 1170-1240)
En 1228 , el Italiano Fibonacci en su obra "Liber Abaco", propone un problema para descubrir la cantidad de descendientes que podrían nacer de una pareja de conejos en el período de un año. De la respuesta a esa pregunta,"1, 1, 2, 3, 5, 8, 13, 21, 34..." ha surgido la "Secuencia Fibonacci"... <

Como se puede observar, cada número se obtiene sumando los dos que le preceden:
Por ejemplo:
1+1=2
2+1=3
3+2=5
5+3=8..."ad infinitum"...
La relación entre el numero áureo y esa secuencia, es que los cocientes (razones) entre dos números de la sucesión, se aproximan más y más al número áureo (1'61803...)segun avanzán hacia el infinito.
En 1753 el matemático escoces Robert Simpson descubrió que la relación entre dos números sucesivos de la secuencia Fibonacci se acerca a la relación áurea phi cuanto más se acerque el numero, al infinito.

Esa sucesión puede empezar en cualquier numero desde que cumpla la condición de
ser el resultado de suma de los dos números anteriores.
Algunos historiadores afirman que esa secuencia ya había sido descubierta antes de 1135, por Gopala y Hemachandra, matemáticos indus.
En los años 1870, el francés Éduard Lucas ha estudiado y encontrado muchas propiedades y aplicaciones para la secuencia que puede ser observada en la perfecta belleza de la naturaleza en sus infinitas manifestaciones a cada momento:

En las formas de flores y hojas así como en la distribución de sus pétalos, semillas y hojas; en las ramas de los arboles y demás fractales; en en el vuelo del cóndor, en la reproducción de los conejos, en la relación entre el numero de abejas machos y hembras de un panal. En algunas proporciones del cuerpo humano, en las olas del mar, en las galaxias, en los sensillos remolinos de agua que desaparecen por el desague cada vez que abrimos el grifo... y mucho más que podrás reconocer como tal a partir de ahora .
El "Hombre de Vitruvio"
Ilustración de Leonardo da Vinci en 1492, basada en las proporciones
humanas descriptas en la obra "De architetura"
del arquitecto MarcusVitruvius (25 aC)
“Vitruvio el arquitecto, dice en su obra sobre arquitectura que la naturaleza distribuye las medidas del cuerpo humano como sigue: que 4 dedos hacen 1 palma, y 4 palmas hacen 1 pie, 6 palmas hacen 1 codo, 4 codos hacen la altura del hombre.Y 4 codos hacen 1 paso, y que 24 palmas hacen un hombre; y estas medidas son las que él usaba en sus edificios.
Si separas la piernas lo suficiente como para que tu altura disminuya 1/14 y estiras y subes los hombros hasta que los dedos estén al nivel del borde superior de tu cabeza, has de saber que el centro geométrico de tus extremidades separadas estará situado en tu ombligo y que el espacio entre las piernas será un triángulo equilátero.
La longitud de los brazos extendidos de un hombre es igual a su altura.
Desde el nacimiento del pelo hasta la punta de la barbilla es la décima parte de la altura de un hombre; desde la punta de la barbilla a la parte superior de la cabeza es un octavo de su estatura; desde la parte superior del pecho al extremo de su cabeza será un sexto de un hombre. Desde la parte superior del pecho al nacimiento del pelo será la séptima parte del hombre completo.
Desde los pezones a la parte de arriba de la cabeza será la cuarta parte del hombre.
La anchura mayor de los hombros contiene en sí misma la cuarta parte de un hombre. Desde el codo a la punta de la mano será la quinta parte del hombre; y desde el codo al ángulo de la axila será la octava parte del hombre.
La mano completa será la décima parte del hombre; el comienzo de los genitales marca la mitad del hombre.
El pie es la séptima parte del hombre.
Desde la planta del pie hasta debajo de la rodilla será la cuarta parte del hombre.
Desde debajo de la rodilla al comienzo de los genitales será la cuarta parte del hombre.
La distancia desde la parte inferior de la barbilla a la nariz y desde el nacimiento del pelo a las cejas es, en cada caso, la misma, y, como la oreja, una tercera parte del rostro».








No hay comentarios:
Publicar un comentario